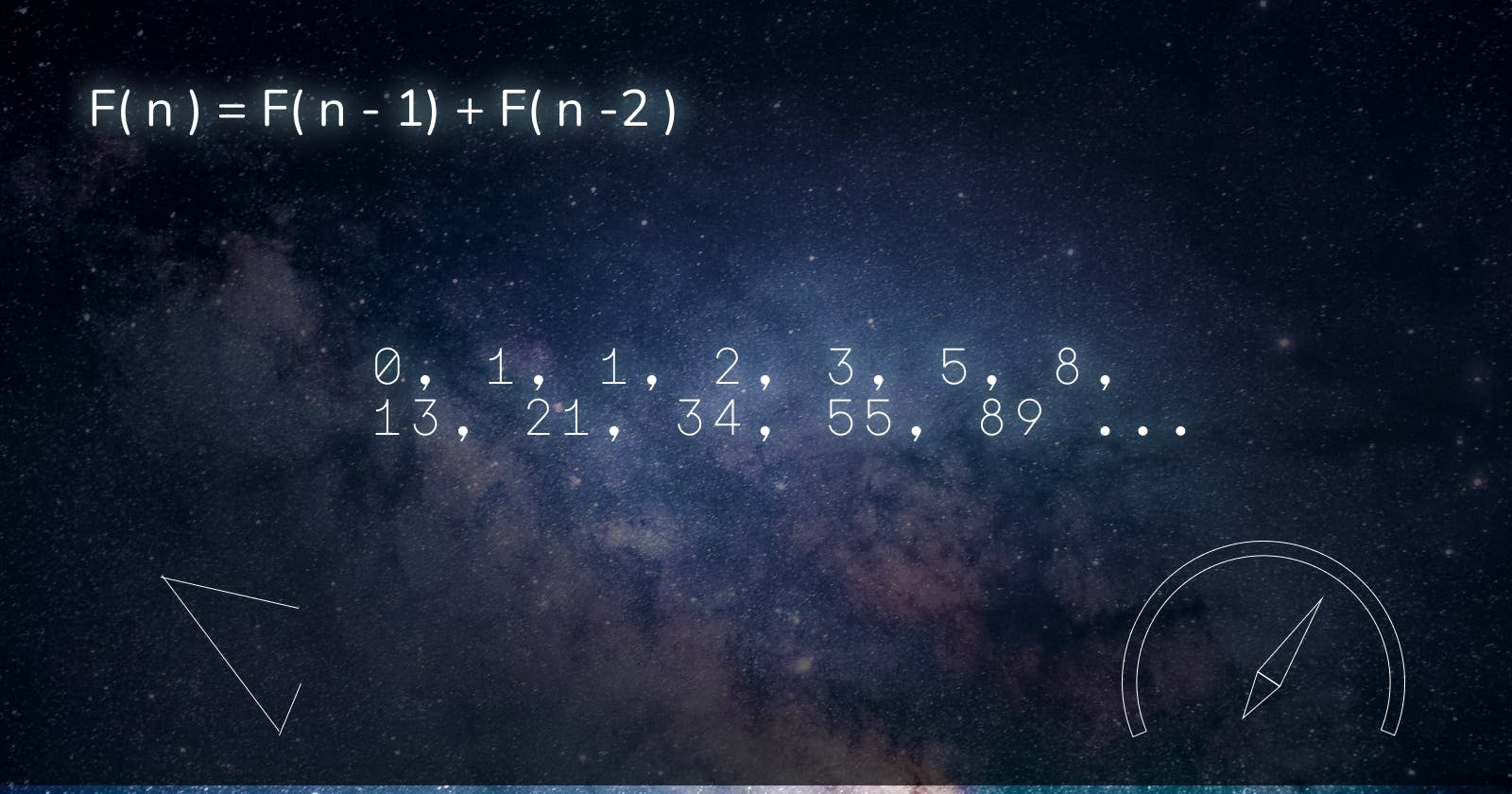Fibonacci sequence

The Fibonacci sequence is a series of numbers in which each number is the sum of the two that precede it. Starting at 0 and 1, the sequence looks like this: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, and so on forever. The Fibonacci sequence can be described using a mathematical equation X(n+2)= X(n+1) + X(n).

Implementation

a simple intuition that comes on our mind to solve this problem is by implementing a recursive function that has the n-th term as a parameter and n <= 2 as a base case.
Let's start writing some code

Let's try and test our function by mesuring the execution time

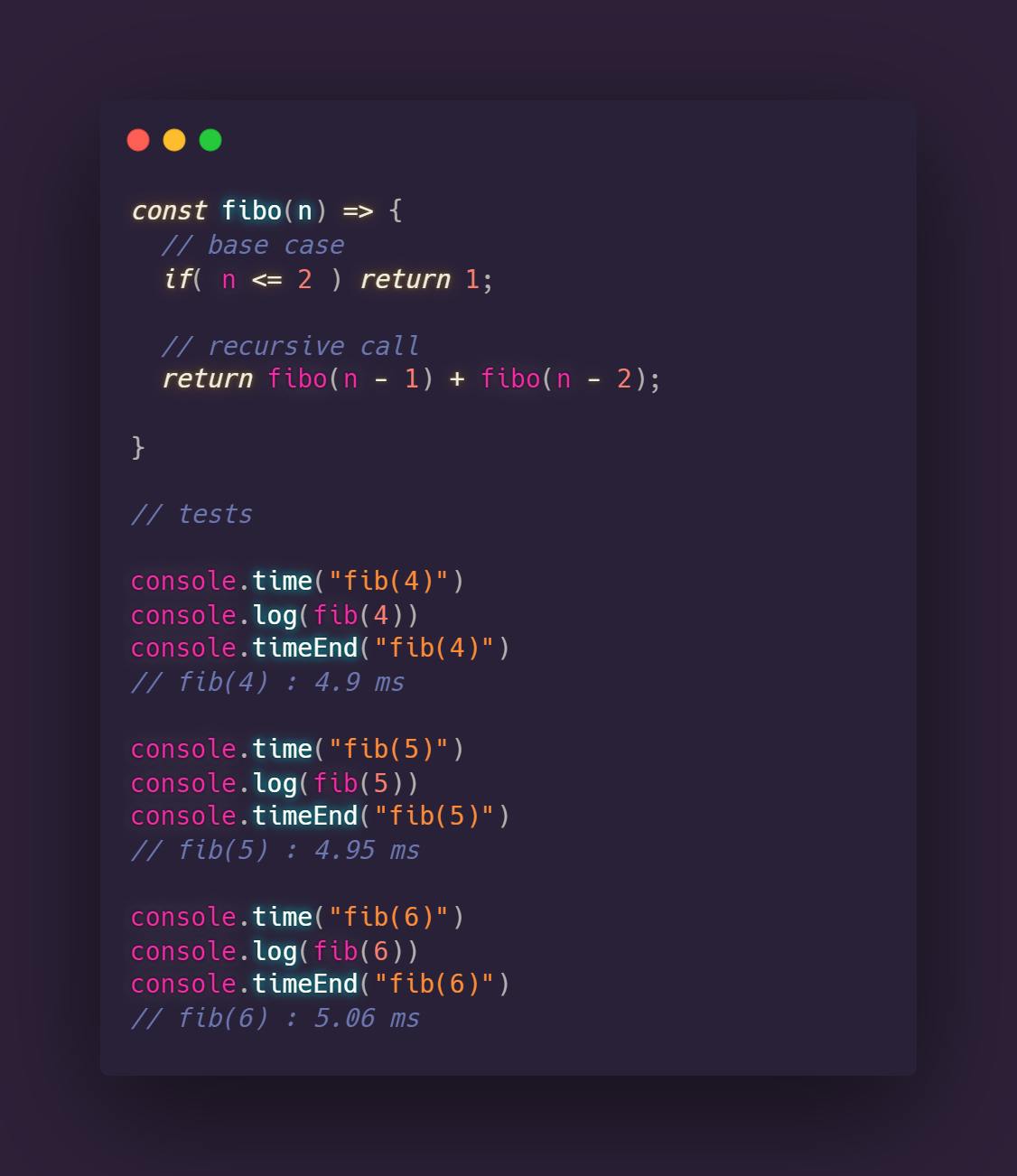That looks pretty good right? Well not until we plug in some bigger numbers. let's try with n = 50 and n = 51

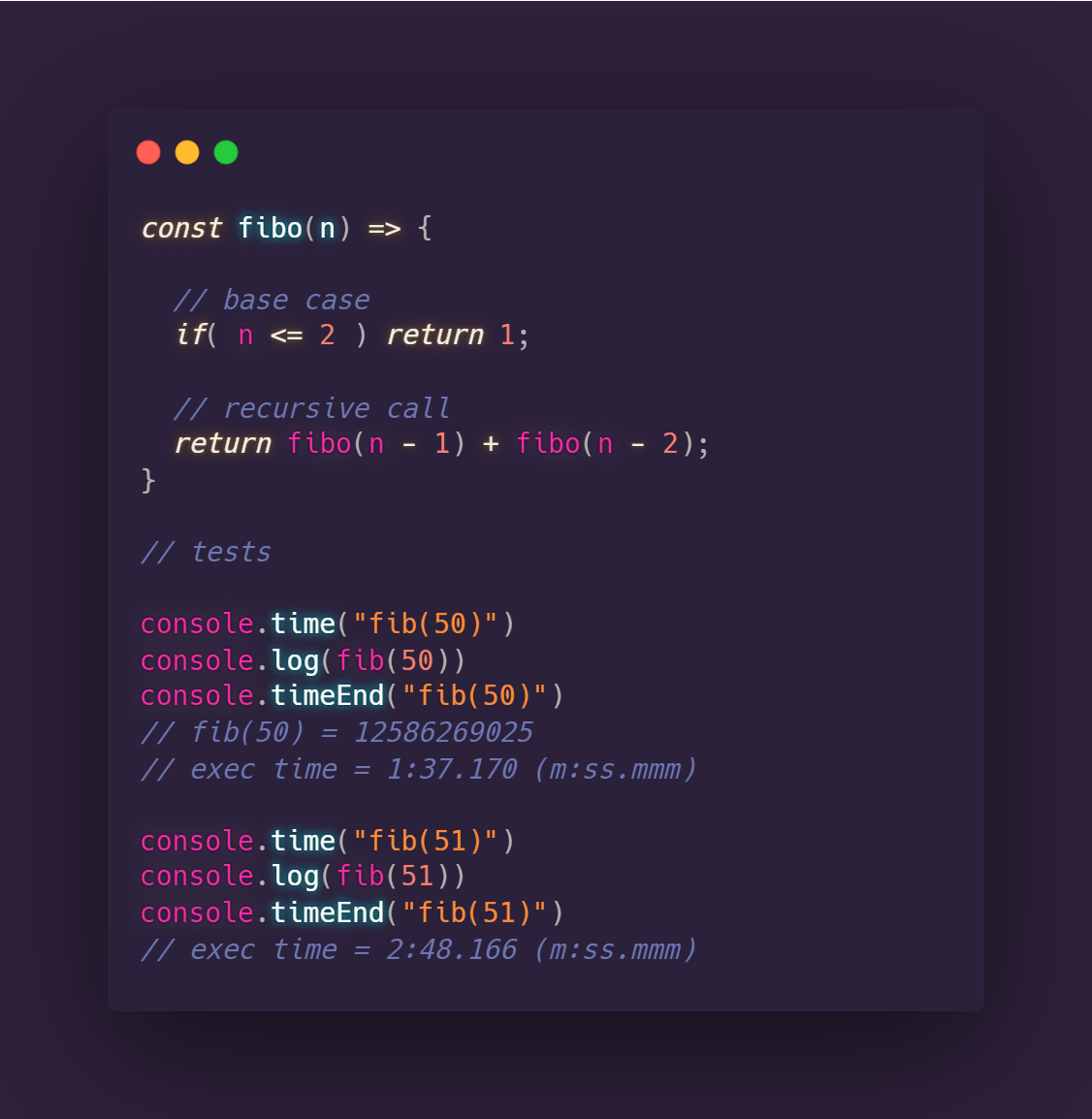
Woah! the function tends to fail miserably in terms of speed when bigger numbers are provided (although technically 50 and 51 are not considered as big numbers), so we can clearly see that this function is quite horrible.
But why does it fail so hard ? Let's try to visualize the call stack to get a better understanding of what's happening under the hood

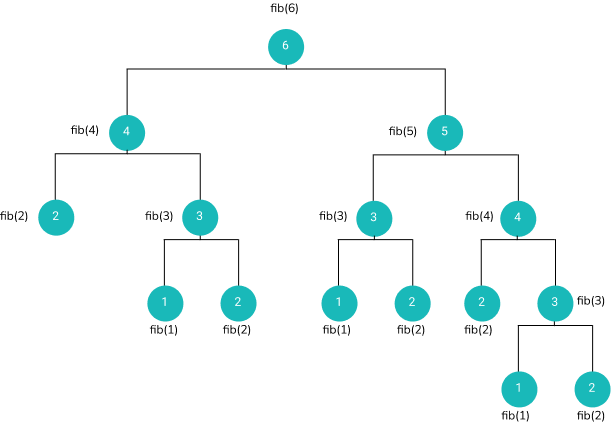In order to compute fib(6) the function tries to compute fib(5) and fib(4) respectively , and to compute fib(5) it has to compute fib(4) and fib(3) and so on (fib(n) = fib(n-1) + fib(n+1)) until it reaches a base case fib(1) = fib(2) = 1 then the result backpropagates to the higher nodes until fib(5) and fib(4) are evaluated.

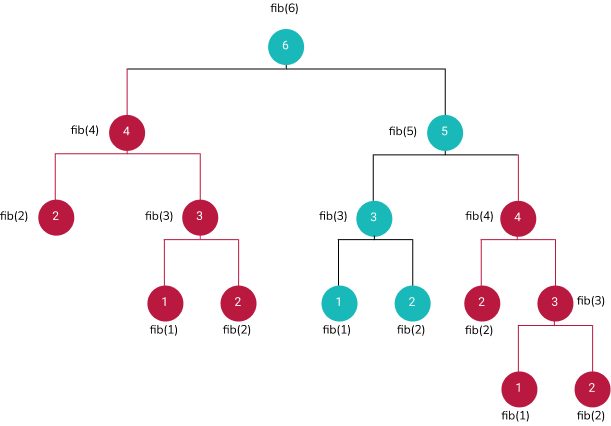By observing the call tree, we can see that there are plenty of duplicated calculations. for example fib(4) is calculated twice, one when evaluating the left child of fib(6) and the other one when evaluating the right child of fib(5) . same thing applies for the node fib(3) so our function is not doing a very good job remembering what It has already calculated but instead it is repeating the same calculations over and over again.
In fact , this algorithm is so bad that it has a complexity of O(2ⁿ)! consequently, to compute fib(50) the processor has to execute 2⁵⁰ operations
(2⁵⁰ = 1 125 899 906 842 624 by the way)
Calculating fib(60) requires 1024 times more operations than fib(50) so an estimated execution time for fib(60) would be 1024 x 1.3(minutes) = 33 hours!

So is there a way to optimize the function ?

Definetly YES! this is where Dynamic Programming comes to the rescue
Dynamic programming is both a mathematical optimization method and a computer programming method, it aims to simplify a complicated problem by breaking it down into simpler sub-problems in a recursive manner.
What bother us the most about the previous recursive implementation are the duplicated calculations , so if we can find a way to store the previously calculated terms, we can vastly improve the performance and obtain a very pleasing execution time.
This is called memoization and it is one of the techniques used in dynamic programming.
So the idea is to store the pre-computed terms in a data structure that allows us to quickly write and read from it like a Heap, Self-balancing tree , hash table ..etc.
I'm gonna be using a javascript object to store the values , where the keys are the terms and the values are the fib(of that term).
Let's jump again and modify the code

We've added another parameter to our function , which is the object that stores the pre-computed values.
We check first if the key exists in the object , if true, we return its value , if not we check if we are in a base case, if not we call the function for n-1 and n-2 while passing the memo object as a parameter.
Notice that we are storing the result of the recursive call in the memo object to prevent duplicated calculations.
Now let's try again for n = 50 and even n = 100

Quite satisfying right ? We have successfully obtained a very very huge acceleration , which made our function incredibly fast even for very large numbers.

Conclusion

Space and time complexity are the key factors when evaluating how good your algorithm is , implementing an algorithm that works is not enough , optimizing it as much as you can has to be your ultimate goal.